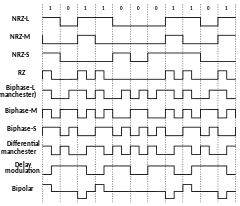
Return-to-zero

Return-to-zero (RZ or RTZ) describes a line code used in telecommunications signals in which the signal drops (returns) to zero between pulses. This takes place even if a number of consecutive 0s or 1s occur in the signal. The signal is self-clocking. This means that a separate clock does not need to be sent alongside the signal, but suffers from using twice the bandwidth to achieve the same data-rate as compared to non-return-to-zero format.
The "zero" between each bit is a neutral or rest condition, such as a zero amplitude in pulse-amplitude modulation (PAM), zero phase shift in phase-shift keying (PSK), or mid-frequency in frequency-shift keying (FSK). That "zero" condition is typically halfway between the significant condition representing a 1 bit and the other significant condition representing a 0 bit.
Although return-to-zero (RZ) contains a provision for synchronization, it still has a DC component resulting in “baseline wander” during long strings of 0 or 1 bits, just like the line code non-return-to-zero.
Return-to-zero in optical communication
[edit]Return to zero, inverted
[edit]Return-to-zero, inverted (RZI) is a method of mapping for transmission. The two-level RZI signal has a pulse (shorter than a clock cycle) if the binary signal is 0, and no pulse if the binary signal is 1. It is used (with a pulse 3/16 of a bit long) by the IrDA serial infrared (SIR) physical layer specification. Required bandwidth for this kind of modulation is: BW = R(data rate).
Bipolar return-to-zero (bipolar RZ)
[edit]For bipolar return-to-zero (bipolar RZ), a binary one is encoded as +V volts, a binary zero is encoded as −V volts, and 0 volt is used to provide padding and separation between bits.
Bipolar return-to-zero encoding is used by the ARINC 429 bus.
See also
[edit]Other line codes that have 3 states:
References
[edit]Further reading
[edit]- Savard, John J. G. (2018) [2006]. "Digital Magnetic Tape Recording". quadibloc. Archived from the original on 2018-07-02. Retrieved 2018-07-16.