Scorer's function
Appearance

In mathematics, the Scorer's functions are special functions studied by Scorer (1950) and denoted Gi(x) and Hi(x).
Hi(x) and -Gi(x) solve the equation
and are given by
The Scorer's functions can also be defined in terms of Airy functions:
It can also be seen, just from the integral forms, that the following relationship holds:
-
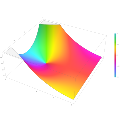
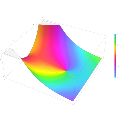
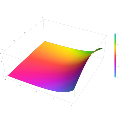
Plot of the Scorer function Gi(z) in the complex plane from -2-2i to 2+2i with colors created with Mathematica 13.1 function ComplexPlot3D
-
Plot of the derivative of the Scorer function Hi'(z) in the complex plane from -2-2i to 2+2i with colors created with Mathematica 13.1 function ComplexPlot3D
-
Plot of the derivative of the Scorer function Gi'(z) in the complex plane from -2-2i to 2+2i with colors created with Mathematica 13.1 function ComplexPlot3D
-
Plot of the Scorer function Hi(z) in the complex plane from -2-2i to 2+2i with colors created with Mathematica 13.1 function ComplexPlot3D
References
[edit]- Olver, F. W. J. (2010), "Scorer functions", in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (eds.), NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248.
- Scorer, R. S. (1950), "Numerical evaluation of integrals of the form and the tabulation of the function ", The Quarterly Journal of Mechanics and Applied Mathematics, 3: 107–112, doi:10.1093/qjmam/3.1.107, ISSN 0033-5614, MR 0037604